Topology

• \(C\subseteq X\) is closed in \((X, \tau)\), if \(X\setminus C \in \tau\) which means it is an open set.

• For a nonempty family of topological space \(\{X_i\}_{i\in I}\),
• The product space is the Cartesian product: \[ X := \prod_{i\in I}X_i \]
• equipped with the product topology, somtimes also called Tychonoff topology, that is defined to be the coarsest topology for which all the canonical projections \(\pi_i^\natural \colon X \to X_i\) are continuous.

• A base for the topology \(\tau\) is a family \(\mathcal{B}\subseteq \tau\) of open sets such that every open set of the topology can be represented as the union of some subfamily of \(\mathcal{B}\).
• Equivalently, a family \(\mathcal{B}\) of subsets of \(X\) is a base for the topology \(\tau\) if and only if \(\mathcal{B}\subseteq \tau\) and \(\forall U\in \tau, \forall x\in U, \exists B\in \mathcal{B}, x\in B\subseteq U\).

• Euclidean spaces are second-countable.
  • to wit, the set of all open balls centered at rational points with rational radii forms the countable base.

• Toposogical space containing a countable dense subset.

• For a point \(p\) in a metric space \((X, d)\), a set \(V\) is a neighborhood of a point \(p\) if there exists an open ball with center \(p\) and radius \(r>0\) contained in \(V\).

• Complete System of Neighborhoods, Neighborhood filter
• \(\mathcal{N}(x)\)
• Collection of all neighborhoods of \(x\).

• Local Basis, Neighborhood Base, Local Base
• A neighborhood basis for a point \(x\) is a filter base of the neighbourhood filter.
  • It is a subset \(\mathcal{B}\subseteq \mathcal{N}(x)\) such that \(\forall V\in \mathcal{N}(x), \exists B\in \mathcal{B}, B\subseteq V\).
• Equivalently, the neighborhood filter \(\mathcal{N}\) can be recovered from \(\mathcal{B}\)
  • \[ \mathcal{N}(x) = \{V\subseteq X\colon \exists B\in \mathcal{B}, B\subseteq V\}. \]
• A family \(\mathcal{B}\in \mathcal{N}(x)\) is a neighborhood basis for \(x\) if and only if \(\mathcal{B}\) is a cofinal subset of \((\mathcal{N}(x), \supseteq)\) with respect to the partial order \(\supseteq\).

• \( f\colon X \to Y \) is a homeomorphism if:
  • \( f \) is a bijection
  • \( f \) is continuous
  • the inverse function \( f^{-1} \) is continuous

• The glued together Möbius strip is homeomorphic to Klein bottle.

• A set \(K\) in topological or metric space is compact, if every open cover of \(K\) has finite subcover.

• Compact set behave like finite set in topological sense.
• It make local properties into a global ones.
  • In extreme value theorem, boundedness of \(f\) in a neighborhood of \(x\in [a, b]\) implies the boundedness of \(f\) on \([a,b]\).

• Equivalently, except few rare cases, every sequence in \(K\) has convergent subsequence.
• This is equivalent to complete and total bounded.
  • This is essentially saying a sequence cannot diverge, has a limit, and cannot escape to infinite dimensions.

• A topological space is called countably compact if every countable open cover has a finite subcover.

• A space is σ-compact if it is the union of countably many compact subspaces.

• Two points in \(X\) are topologically distinguishable, if at least one of them has a neighborhood that is not a neighborhood of the other.

• Two points are separated if each of them has a neighborhood that is not a neighborhood of the other.

• For subsets \(A\) and \(B\):

• T_• are the Kolmogorov Classification.
• Inverse Hasse diagram
• 
  • P: Perfectly, C: Completely, N: Normal, R: Regular
  • Non-T₀ on the left, T₀ on the right.
  • The Kolmogorov quotient, quotient space under the equivalence relation of topological indistinguishability, of the left side is the right side.
  • If a space satisfies two axioms simultaneously, then the space satisfies all the axioms up to the supremum of the two.

• A space \(X\) is said to be first-countable if each point has a countable neighborhood basis.

• A topological space \(X\) whose topology has a countable base.

• Euclidean space with its usual topology is second-countable.
• The long ray is \(\omega_1\times [0,1)\) equipped with the order topology that arises from the lexicographical order on \(\omega_1\times [0,1)\).
  • It is second-uncountable, but is first-countable.

A topological space \(M\) is a manofold if:

• Either paracompact or second-countable: The space is not pathologically large.
• Hausdorff: Distinct points are seperable by neighborhoods.
• Locally Euclidean: Every point has a neighborhood homeomorphic to an open subset of the Euclidean space.

• See differentiable manifold.
• A manifold is differentiable, when the transition maps are differentiable.
• Furthermore, if the transition maps are smooth then the atlas is smooth atlas, and the manifold is itself smooth.

• All manifolds are topological manifold.

• Riemannian Surface
• \((M, g)\)

• Manifold with an atlas of charts to the open unit disc in \(\mathbb{C}^n\) , such that the transition maps are holomorphic.
• Intuitively, complex differentiable manifold.

• CR Manifold

• \((E, B, \pi, F)\)
• \(F\longrightarrow E \xrightarrow{\pi} B\)
  • In analogy with a exact sequence
• The base space \(B\) is a connected topological space, and the total space \(E\) and the fiber \(F\) are topological spaces, and the map \(\pi\colon E\to B\) is a continuous surjection satisfying a local triviality:
  • For every \(x\in B\), there exists an open neighborhood \(U\subseteq B\) of \(x\), called trivializing neighborhood, such that there exists a homeomorphism \(\varphi\) for the following commutative diagram:
  • 
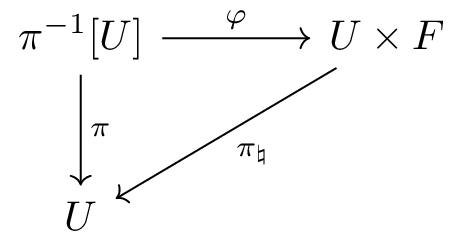
  • where \(\pi^{-1}[U]\) is given the subspace topology, and \(U\times F\) is given the product topology, and \(\pi_\natural\) is the natural projection.

• Submersion

The union \( \cup_k X_k \) of a sequence of topological spaces \[ \varnothing = X_{-1} \subset X_0 \subset X_1 \subset \cdots \] such that each \( X_k \) is gluing of copies of \( k \)-cells \( (e_{\alpha}^k)_{\alpha} \) to \( X_{k-1} \) by continuous attaching map \( g_{\alpha}^k \colon \partial e_{\alpha}^k \to X_{k-1} \). Note that \( k \)-cell \( e_{\alpha}^k \) is each homeomorphic to the open \( k \)-ball.

Each \( X_k \) is called the k-skeleton of the complex.

• 0-dimensioanl
  • Every discrete topological space
• 1-dimensional
  • Interval
  • Circle
  • Graph
• Finite-dimensional
  • n-dimensional sphere
  • n-dimensional real projective space
  • Polyhedra
  • Differentiable Manifolds

m-chain is a formal linear combination of m-cells: \[ \Sigma = \sum_i n_i \sigma_i \] defined to follow the integration rule \[ \int_{\Sigma} \omega = \sum_i n_i \int_{\sigma_{i}} \omega. \]

• For any finite CW-complex, the Euler characteristic can be defined as the alternating sum: \[ \chi = k_0 - k_1 + k_2 - k_3 + \cdots \] where \(k_n\) denotes the number of cells of dimension \(n\) in the complex.

• Any surface of a convex polyhedron has Euler characteristic of 2: \[ \chi = V - E + F = 2. \]